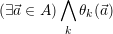
The solver provides a special algorithm for constraints of the form
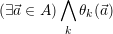
where θk(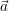 ) is either of the form ∑
iciai + di = 0, or of the form
) is either of the form ∑
iciai + di = 0, or of the form
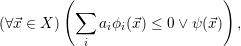
where ϕi(x) and ψ(x) may be an arbitrary Boolean combination of constraints,
but they are only allowed to contain the variables 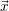 .
.
For using this algorithm, RSolver has to be called using the parameters -f Sample -p DeductionStrategy RelaxationUniv, and the existential quantifier has to be written in the variant EXISTS*. See the examples in the directory examples/relax of the distribution.
The corresponding algorithm exploits the fact that the ai only occur linearly. This allows solving the problem using linear-programming relaxations [16].